

In algebra, it is important to understand the behavior of quadratic functions and their graphs. This short guide will cover the following key concepts (including examples):
A quadratic function in standard form looks like this: f(x)=ax^2+bx+c, where a, b, and c are constants. You can also express a quadratic function in standard form as y=ax^2+bx+c (note that we will be using f(x)= and y= interchangeable in this guide). Graphing a parabola on the coordinate plane by using its formula is an important algebra skill and this lesson guide will teach you a simple 3-step process that you can use for graphing a parabola in almost any scenario.
Before you learn how to graph a parabola in standard form, let’s review some key concepts and vocabulary related to quadratic functions and their graphs before moving onto a few graphing parabolas examples.
A quadratic function in standard form is a function that looks like this: f(x)=ax^2+bx+c.
For example, for the standard form quadratic f(x)=x^2 -4x + 5, a=1, b=-4, and c=5
The graph of a function is a parabola—a U-shaped plane curve that is symmetrical about a line of symmetry that passes through a vertex point. A parabola is symmetrical and forms a mirror image of itself on opposite sides of the line of symmetry that passes through the vertex point.
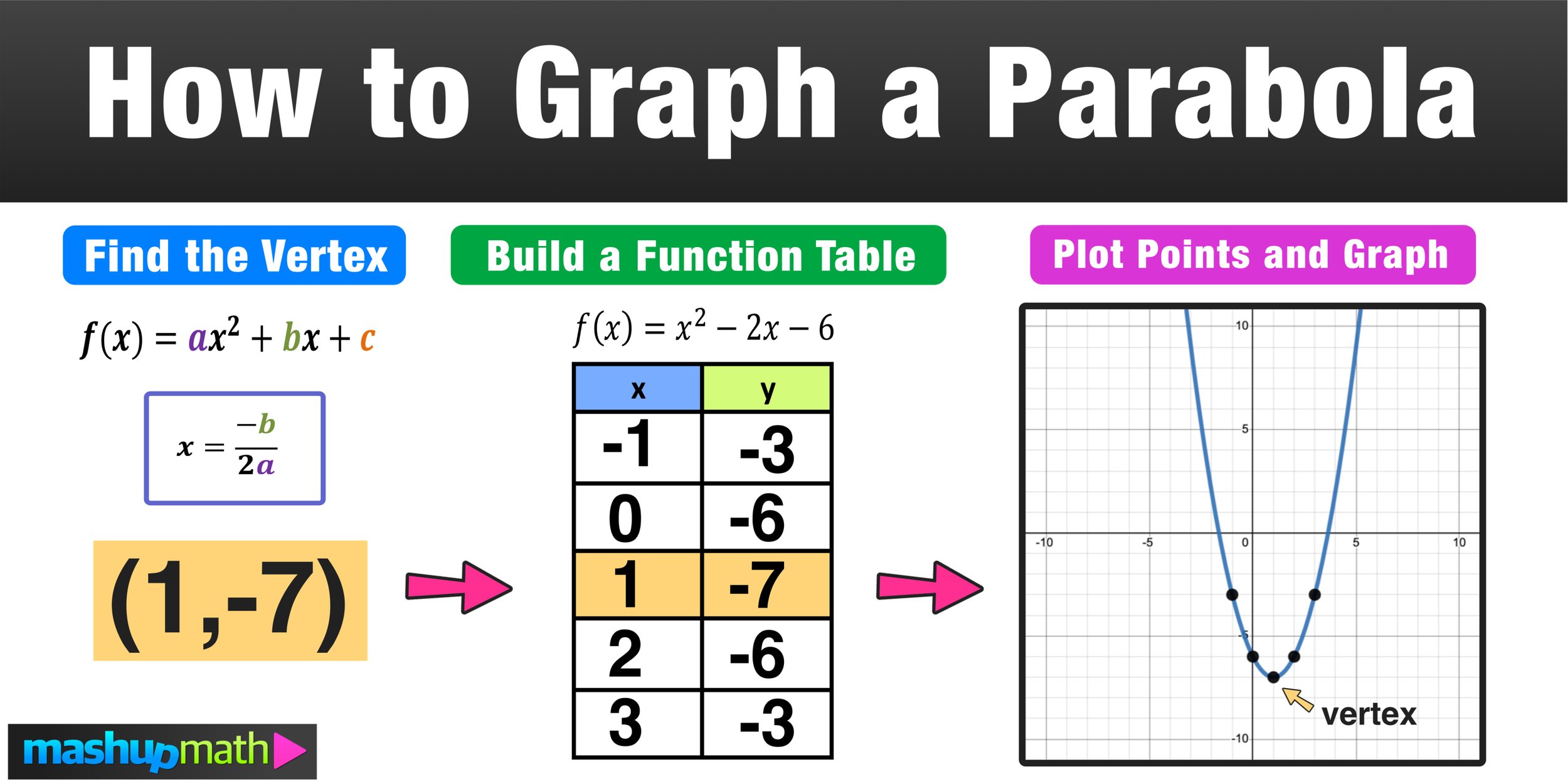
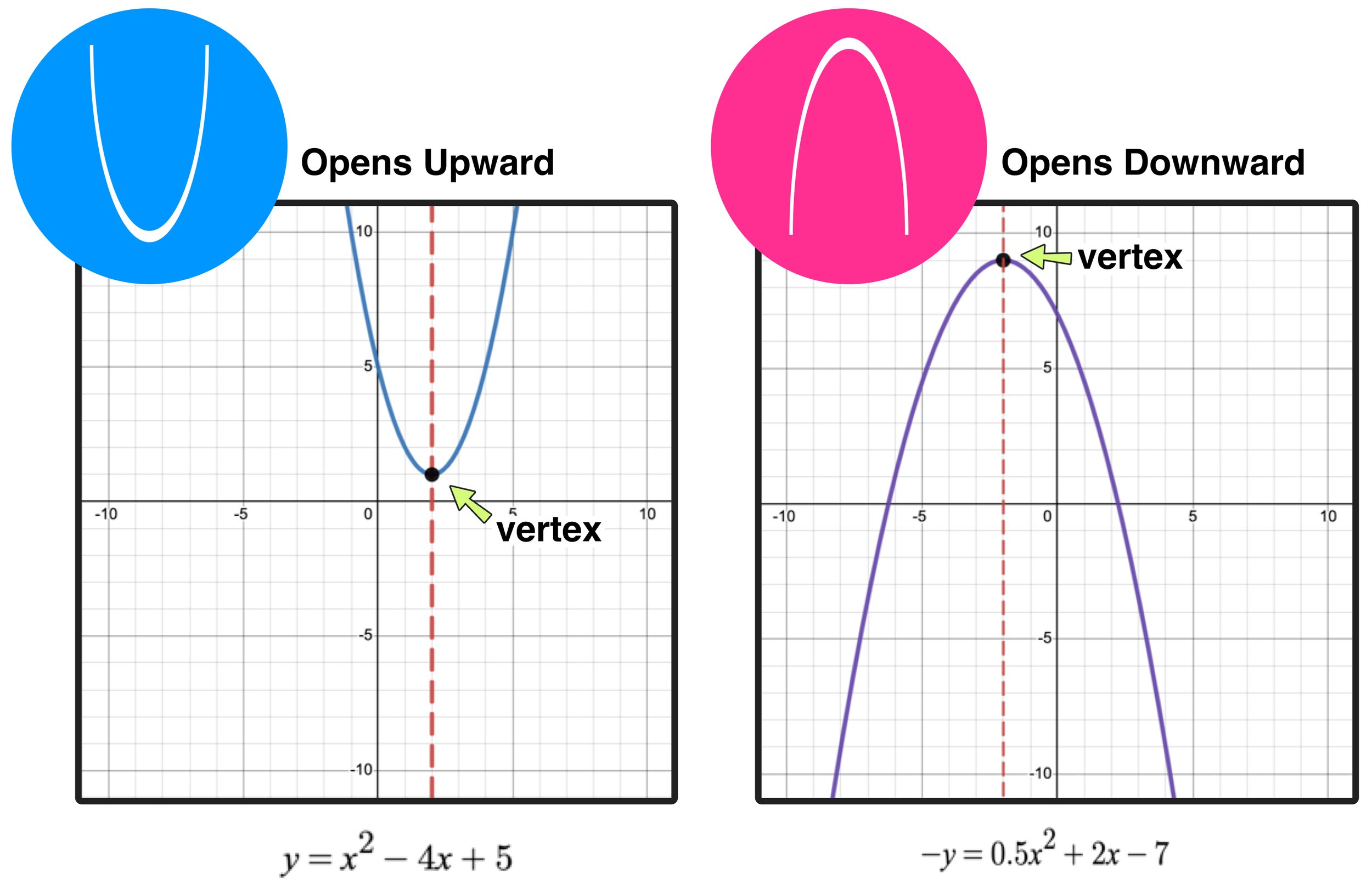
Figure 01 below shows examples of quadratic functions in standard form along with a corresponding graph. Notice the U-shape parabola for each graph along with the vertex point. Also notice that a parabola can open upward (U-shaped) or open downward (upside-down U-shaped).
Now that you know what the graph of a quadratic function in standard form looks like, let’s take a further look at what the vertex of a parabola is.
The vertex of a parabola is the (x,y) coordinate point where a parabola and its axis of symmetry intersect.
In Figure 01 above, the vertex of a parabola is labeled and the axis of symmetry is the horizontal dashed line that passes through it.
In simpler terms, what is the vertex of a parabola? The vertex is the point at the very bottom of the curve for parabolas that open upward or at the very top of the curve for parabolas that open downward.
If you can find the vertex of a parabola, then you can easily learn how to graph a parabola on the coordinate plane, so understanding what is the vertex of a parabola and how to find it is key. Luckily, finding the vertex of a parabola is easy to do as long as you follow two simple steps:
To find the vertex of a parabola in f(x)=ax^2+bx+c form:
The key concepts of what is the vertex of a parabola and how to find the vertex of a parabola is shown in Figure 02 below.